Prior to exploring the implications of chaos in respect of human behaviour, and to assist in greater understanding, I will briefly introduce two subjects that are important in unpacking the world of chaos.
These are fractal geometry and its hallmark self-similarity.
(The Polish/French mathematician Benoit Mandelbrot introduced the notion of fractal geometry and a wide variety of literature is available on the rather complicated mathematical theories if you are interested).
For our purposes I will define a fractal as a pattern that repeats itself through time. Here is one explanation/demonstration of fractals on Youtube and there are many others if you want to search.
A simple example of the manifestation of both fractal geometry and self-similarity in nature is the growth of a tree.
We see a trunk, surrounded by sturdy branches, from which smaller branches emerge, with still smaller branches from those, and then twigs, smaller twigs, and then leaves, and within the leaves are capillaries from which smaller capillaries emerge.
The fractal part is the breaking up of the main trunk into smaller branches and still smaller and so on. The self-similarity part is a (relatively recently worked out mathematically, but observed since the dawn of humanity) symmetry in nature where the overall pattern of the fractal is repeated at multiple scales.
That is, even a very small twig from which grows even smaller twigs will be similar to (but, and importantly, not exactly the same as) the trunk itself from which grows the branches [1]. The chaos part comes in when we consider that we cannot predict from looking at an acorn what exactly the oak tree will look like in a hundred years’ time. But despite our not knowing what it will exactly look like, we know that it will follow a particular pattern as it grows – and not turn out like a sycamore tree, or a head of cabbage!
Like snowflakes, (which are actually more amazing as they are not growing – but that is another story) all trees are alike but all are different also.
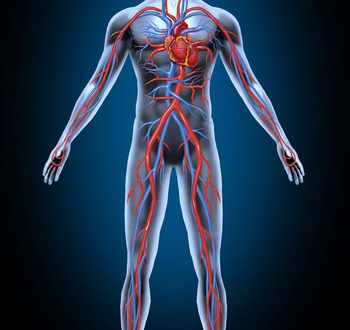
Another example is blood flow in our body. We observe the heart from which extends the aorta, the biggest and most important artery, surrounded by big arteries to the principal organs from which emanate smaller arteries and then even smaller ones again and then capillaries and then the tiniest of blood vessels close to the skin.
Here are some pictures (nowadays called images for some reason) of self-similarity in nature. The first is a fern leaf, the second portrays blood flow in our body, and the third is an elderberry twig.
The self-similarity can be clearly seen in the pictures.


Once again let us look at our oak tree. The tree, starting from an acorn, will get nourishment and sustenance from water and soil but once it breaks through the soil it will get energy, nourishment etc. from the sunlight and moisture from rain on its leaves.
When I consider fractals and self-similarity in nature, I always factor in growth!
As it grows bigger and bigger it is dependent on both to grow – if the ground dried up, or the soil turned to sand, or the sun stopped shining or the rain stopped falling, the tree would stop growing.
This implies that growth is dependent on the strength and solidity of the trunk, what I will call the centre of growth and the fragile, delicate and barely visible capillaries on the extremities of the leaves – what I will call the edge of growth. I will link these terms to society and family in a following post.
[1]. The differences between the individual branches, twigs, leaves etc. can be described by a mathematical property called non-linearity. If it was generated by a computer instead of growing in nature, the fractal could be exactly the same, as it could be given linear properties by the person who created the programme. If you type computer generated fractals into a You-tube search you will find loads. They can have a hypnotic effect.
